Skip to content

Pacbio reads: assembly with command line tools

Keywords: de novo assembly, PacBio, PacificBiosciences, Illumina, command line, Canu, Circlator, BWA, Spades, Pilon, Microbial Genomics Virtual Laboratory

This tutorial demonstrates how to use long Pacbio sequence reads to assemble a bacterial genome, including correcting the assembly with short Illumina reads.

Author Information

Primary Author(s): Anna Syme Melbourne Bioinformatics

Resources

Tools (and versions) used in this tutorial include:

  • canu 1.5 [recently updated]
  • infoseq and sizeseq (part of EMBOSS) 6.6.0.0
  • circlator 1.5.1 [recently updated]
  • bwa 0.7.15
  • samtools 1.3.1
  • makeblastdb and blastn (part of blast) 2.4.0+
  • pilon 1.20

Learning objectives

At the end of this tutorial, be able to:

  1. Assemble and circularise a bacterial genome from PacBio sequence data.
  2. Recover small plasmids missed by long read sequencing, using Illumina data
  3. Explore the effect of polishing assembled sequences with a different data set.

Overview

Simplified version of workflow:

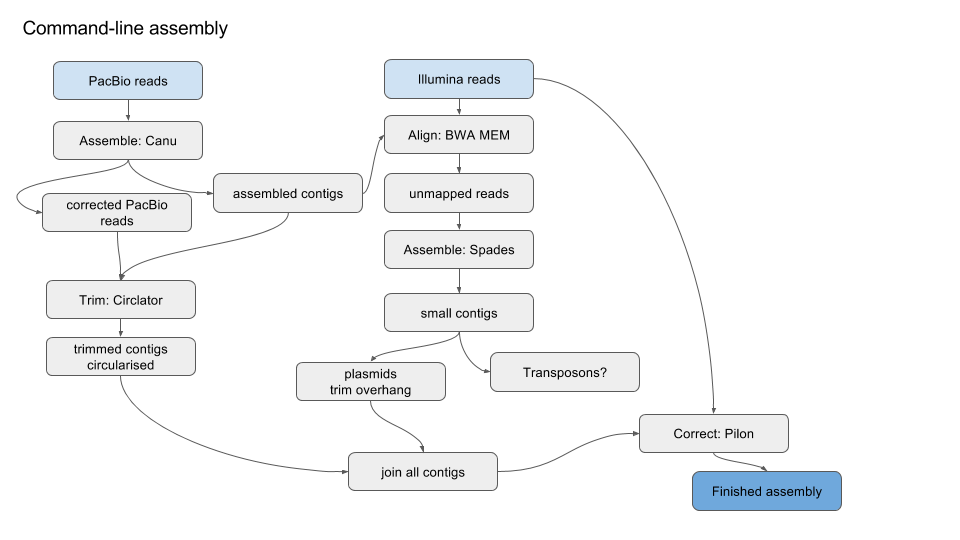
workflow

Prepare the environment

mkdir ~/denovo-canu
cd ~/denovo-canu

Get data

The files we need are here [ In a new tab, go to https://doi.org/10.5281/zenodo.1009308]:

  • pacbio.fq : the PacBio reads
  • R1.fq: the Illumina forward reads
  • R2.fq: the Illumina reverse reads

If you already have the files, skip forward to next section, Assemble.

Otherwise, this section has information about how to find and move the files:

PacBio and Illumina files

In a new tab, go to https://doi.org/10.5281/zenodo.1009308.

Next to the first file, right-click (or control-click) the “Download” button, and select “Copy link address”. Back in your terminal, enter

wget  [paste link URL for file]
The file should download. Note: paste the link to the file, not to the webpage. Repeat this for the other two files. Shorten each of these files names with the mv command:

mv R1.fq\?download\=1 R1.fq
mv R2.fq\?download\=1 R2.fq
mv pacbio.fq\?download\=1 pacbio.fq

Type in ls to check the files are present and correctly-named.

We should have R1.fq, R2.fq and pacbio.fq.

cd denovo-canu
ls

Sample information

The sample used in this tutorial is a gram-positive bacteria called Staphylococcus aureus (sample number 25747). This particular sample is from a strain that is resistant to the antibiotic methicillin (a type of penicillin). It is also called MRSA: methicillin-resistant Staphylococcus aureus. It was isolated from (human) blood and caused bacteraemia, an infection of the bloodstream.

Assemble

  • We will use the assembly software called Canu.
  • Run Canu with these commands:
canu -p canu -d canu_outdir genomeSize=0.03m -pacbio-raw pacbio.fq
  • the first canu tells the program to run
  • -p canu names prefix for output files (“canu”)
  • -d canu_outdir names output directory (“canu_outdir”)

  • genomeSize only has to be approximate.

    • e.g. Staphylococcus aureus, 2.8m
    • e.g. Streptococcus pyogenes, 1.8m
    • (In this case we are using a partial genome of expected size 30,000 base pairs).

  • Canu will correct, trim and assemble the reads.

  • Various output will be displayed on the screen.

Check the output

Move into canu_outdir and ls to see the output files.

  • The canu.contigs.fasta are the assembled sequences.
  • The canu.unassembled.fasta are the reads that could not be assembled.
  • The canu.correctedReads.fasta.gz are the corrected Pacbio reads that were used in the assembly.
  • The canu.file.gfa is the graph of the assembly.
  • Display summary information about the contigs: (infoseq is a tool from EMBOSS)
infoseq canu.contigs.fasta
  • This will show the contigs found by Canu. e.g.,
    - tig00000001   47997
  • This will show the contigs found by Canu. e.g., tig00000001 47997 -“tig00000001” is the name given to the contig -“47997” is the number of base pairs in that contig.

This matches what we were expecting for this sample (approximately 30,000 base pairs). For other data, Canu may not be able to join all the reads into one contig, so there may be several contigs in the output.

We should also look at the canu.report. To do this:

less canu.report
- less is a command to display the file on the screen. - Use the up and down arrows to scroll up and down. - You will see lots of histograms of read lengths before and after processing, final contig construction, etc. - For a description of the outputs that Canu produces, see: http://canu.readthedocs.io/en/latest/tutorial.html#outputs - Type q to exit viewing the report

Change Canu parameters if required

If the assembly is poor with many contigs, re-run Canu with extra sensitivity parameters; e.g. 

canu -p prefix -d outdir corMhapSensitivity=high corMinCoverage=0 genomeSize=.03m -pacbio-raw pacbio.fq

Questions

Q: How do long- and short-read assembly methods differ? A: short reads: De Bruijn graphs; long reads: a move back towards simpler overlap-layout-consensus methods.

Q: Where can we find out the what the approximate genome size should be for the species being assembled? A: NCBI Genomes - enter species name - click on Genome Assembly and Annotation report - sort table by clicking on the column header Size (Mb) - look at range of sizes in this column.

Q: In the assembly output, what are the unassembled reads? Why are they there?

Q: What are the corrected reads? How did canu correct the reads?

Q: Where could you view the output .gfa and what would it show?

Trim and circularise

Run Circlator

Circlator identifies and trims overhangs (on chromosomes and plasmids) and orients the start position at an appropriate gene (e.g. dnaA). It takes in the assembled contigs from Canu, as well as the corrected reads prepared by Canu.

Overhangs are shown in blue:

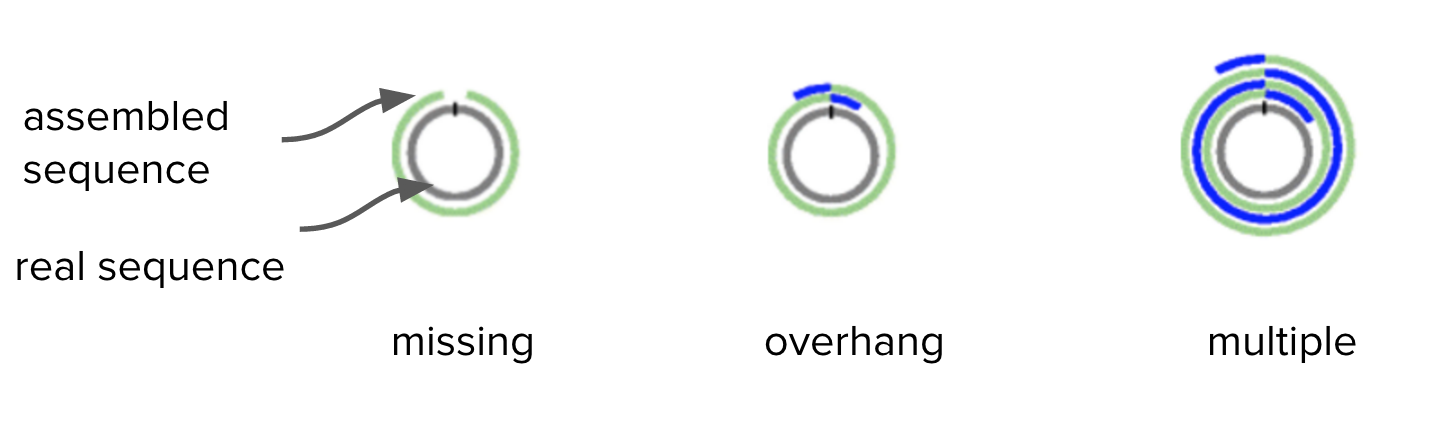circlator Adapted from Figure 1. Hunt et al. Genome Biology 2015

Move back into your main analysis folder.

Run Circlator:

circlator all --threads 8 --verbose canu_outdir/canu.contigs.fasta canu_outdir/canu.correctedReads.fasta.gz circlator_outdir
  • --threads is the number of cores: change this to an appropriate number
  • --verbose prints progress information to the screen
  • canu_outdir/canu.contigs.fasta is the file path to the input Canu assembly
  • canu_outdir/canu.correctedReads.fasta.gz is the file path to the corrected Pacbio reads - note, fastA not fastQ
  • circlator_outdir is the name of the output directory.

Some output will print to screen. When finished, it should say “Circularized x of x contig(s)”.

Check the output

Move into the circlator_outdir directory and ls to list files.

Were the contigs circularised? :

less 04.merge.circularise.log
  • Yes, the contig was circularised (last column).
  • Type “q” to exit.

Where were the contigs oriented (which gene)? :

less 06.fixstart.log
- Look in the “gene_name” column. - The contig has been oriented at tr|A0A090N2A8|A0A090N2A8_STAAU, which is another name for dnaA. This is typically used as the start of bacterial chromosome sequences.

What are the trimmed contig sizes? :

infoseq 06.fixstart.fasta
  • tig00000001 30019 (bases trimmed)

This trimmed part is the overlap.

Re-name the contigs file:

  • The trimmed contigs are in the file called 06.fixstart.fasta.
  • Re-name it contig1.fasta:
mv 06.fixstart.fasta contig1.fasta

Open this file in a text editor (e.g. nano: nano contig1.fasta) and change the header to “>chromosome”.

Move the file back into the main folder (mv contig1.fasta ../).

Options

If all the contigs have not circularised with Circlator, an option is to change the --b2r_length_cutoff setting to approximately 2X the average read depth.

Questions

Q: Were all the contigs circularised? Why/why not?

Q: Circlator can set the start of the sequence at a particular gene. Which gene does it use? Is this appropriate for all contigs? A: Uses dnaA for the chromosomal contig. For other contigs, uses a centrally-located gene. However, ideally, plasmids would be oriented on a gene such as repA. It is possible to provide a file to Circlator to do this.

Find smaller plasmids

Pacbio reads are long, and may have been longer than small plasmids. We will look for any small plasmids using the Illumina reads.

This section involves several steps:

  1. Use the Canu+Circlator output of a trimmed assembly contig.
  2. Map all the Illumina reads against this Pacbio-assembled contig.
  3. Extract any reads that didn’t map and assemble them together: this could be a plasmid, or part of a plasmid.
  4. Look for overhang: if found, trim.

Align Illumina reads to the PacBio contig

  • Index the contigs file:
bwa index contig1.fasta
  • Align Illumina reads using using bwa mem:
bwa mem -t 8 contig1.fasta R1.fq R2.fq | samtools sort > aln.bam
  • bwa mem is the alignment tool
  • -t 8 is the number of cores: choose an appropriate number
  • contig1.fasta is the input assembly file
  • R1.fq R2.fq are the Illumina reads
  • | samtools sort pipes the output to samtools to sort
  • > aln.bam sends the alignment to the file aln.bam

Extract unmapped Illumina reads

  • Index the alignment file:
samtools index aln.bam
  • Extract the fastq files from the bam alignment - those reads that were unmapped to the Pacbio alignment - and save them in various “unmapped” files:
samtools fastq -f 4 -1 unmapped.R1.fastq -2 unmapped.R2.fastq -s unmapped.RS.fastq aln.bam
  • fastq is a command that coverts a .bam file into fastq format
  • -f 4 : only output unmapped reads
  • -1 : put R1 reads into a file called unmapped.R1.fastq
  • -2 : put R2 reads into a file called unmapped.R2.fastq
  • -s : put singleton reads into a file called unmapped.RS.fastq
  • aln.bam : input alignment file

We now have three files of the unampped reads: unmapped.R1.fastq, unmapped.R2.fastq, unmapped.RS.fastq.

Assemble the unmapped reads

  • Assemble with Spades:
spades.py -1 unmapped.R1.fastq -2 unmapped.R2.fastq -s unmapped.RS.fastq --careful --cov-cutoff auto -o spades_assembly
  • -1 is input file forward
  • -2 is input file reverse
  • -s is unpaired
  • --careful minimizes mismatches and short indels
  • --cov-cutoff auto computes the coverage threshold (rather than the default setting, “off”)
  • -o is the output directory

Move into the output directory (spades_assembly) and look at the contigs:

cd spades_assembly
infoseq contigs.fasta
- 1 contig has been assembled with a length of 2359 bases. - Type “q” to exit.

Copy it to a new file:

cp contigs.fasta contig2.fasta

Trim the plasmid

To trim any overhang on this plasmid, we will blast the start of contig2 against itself.

  • Take the start of the contig:
head -n 10 contig2.fasta > contig2.fa.head
  • head -n 10 takes the first ten lines of contig2.fasta
  • > sends that output to a new file called contig2.fa.head
  • We want to see if it matches the end (overhang).
  • Format the assembly file for blast:
makeblastdb -in contig2.fasta -dbtype nucl

  • Blast the start of the assembly (.head file) against all of the assembly: 

    blastn -query contig2.fa.head -db contig2.fasta -evalue 1e-3 -dust no -out contig2.bls

  • blastn is the tool Blast, set as blastn to compare sequences of nucleotides to each other

  • query sets the input sequence as contig2.fa.head
  • db sets the database as that of the original sequence contig2.fasta. We don’t have to specify the other files that were created when we formatted this file, but they need to present in our current directory.
  • evalue is the number of hits expected by chance, here set as 1e-3
  • dust no turns off the masking of low-complexity regions

  • out sets the output file as contig2.bls

  • Look at contig2.bls to see hits:

less contig2.bls
  • The first hit is at start, as expected. We can see that “Query 1” (the start of the contig) is aligned to “Sbject 1” (the whole contig), for the first 540 bases.
  • Scroll down with the down arrow.
  • The second hit shows “Query 1” (the start of the contig) also matches to “Sbject 1” (the whole contig) at position 2253, all the way to the end, position 2359.
  • This is the overhang.
  • Trim to position 2252.
  • Index the plasmid.fa file:

First, change the name of the contig within the file:

nano contig2.fasta
- nano opens up a text editor. - Use the arrow keys to navigate. (The mouse won’t work.) - At the first line, delete the text, which will be something like >NODE_1_length_2359_cov_3.320333 - Type in >contig2 - Don’t forget the > symbol - Press Control-X - Save modified buffer ? - type Y - Press the Enter key

Index the file (this will allow samtools to edit the file as it will have an index): 

samtools faidx contig2.fasta

  • Trim the contig: 
    samtools faidx contig2.fasta plasmid:1-2252 > plasmid.fa.trimmed

  • plasmid is the name of the contig, and we want the sequence from 1-2252.

  • Open this file in nano (nano plasmid.fa.trimmed) and change the header to “>plasmid”, save.

  • We now have a trimmed plasmid.
  • Move file back into main folder:
cp plasmid.fa.trimmed ../
  • Move into the main folder.

Plasmid contig orientation

The bacterial chromosome was oriented at the gene dnaA. Plasmids are often oriented at the replication gene, but this is highly variable and there is no established convention. Here we will orient the plasmid at a gene found by Prodigal, in Circlator:

circlator fixstart plasmid.fa.trimmed plasmid_fixstart
  • fixstart is an option in Circlator just to orient a sequence.
  • plasmid.fa.trimmed is our small plasmid.
  • plasmid_fixstart is the prefix for the output files.

View the output:

less plasmid_fixstart.log
  • The plasmid has been oriented at a gene predicted by Prodigal, and the break-point is at position 1200.
  • Change the file name:
cp plasmid_fixstart.fasta contig2.fasta

Collect contigs

cat contig1.fasta contig2.fasta > genome.fasta

  • See the contigs and sizes: 

    infoseq genome.fasta

  • chromosome: 2823331

  • plasmid: 2473

Questions

Q: Why is this section so complicated? A: Finding small plasmids is difficult for many reasons! This paper has a nice summary: On the (im)possibility to reconstruct plasmids from whole genome short-read sequencing data. doi: https://doi.org/10.1101/086744

Q: Why can PacBio sequencing miss small plasmids? A: Library prep size selection

Q: We extract unmapped Illumina reads and assemble these to find small plasmids. What could they be missing? A: Repeats that have mapped to the PacBio assembly.

Q: How do you find a plasmid in a Bandage graph? A: It is probably circular, matches the size of a known plasmid, has a rep gene…

Q: Are there easier ways to find plasmids? A: Possibly. One option is the program called Unicycler which may automate many of these steps. https://github.com/rrwick/Unicycler

Correct

We will correct the Pacbio assembly with Illumina reads.

Make an alignment file

  • Align the Illumina reads (R1 and R2) to the draft PacBio assembly, e.g. genome.fasta:
bwa index genome.fasta
bwa mem -t 32 genome.fasta illumina_R1.fastq.gz illumina_R2.fastq.gz | samtools sort > aln.bam

  • -t is the number of cores: set this to an appropriate number. (To find out how many you have, grep -c processor /proc/cpuinfo).

  • Index the files:

samtools index aln.bam
samtools faidx genome.fasta
  • Now we have an alignment file to use in Pilon: aln.bam

Run Pilon

  • Run:
pilon --genome genome.fasta --frags aln.bam --output pilon1 --fix all --mindepth 0.5 --changes --verbose --threads 32
  • --genome is the name of the input assembly to be corrected
  • --frags is the alignment of the reads against the assembly
  • --output is the name of the output prefix
  • --fix is an option for types of corrections
  • --mindepth gives a minimum read depth to use
  • --changes produces an output file of the changes made
  • --verbose prints information to the screen during the run
  • --threads : set this to an appropriate number

Look at the changes file:

less pilon1.changes

Example:

pilon

Look at the details of the fasta file:

infoseq pilon1.fasta
  • chromosome - 2823340 (net +9 bases)
  • plasmid - 2473 (no change)

Option:

If there are many changes, run Pilon again, using the pilon1.fasta file as the input assembly, and the Illumina reads to correct.

Genome output

  • Change the file name:
cp pilon1.fasta assembly.fasta
  • We now have the corrected genome assembly of Staphylococcus aureus in .fasta format, containing a chromosome and a small plasmid.

Questions

Q: Why don’t we correct earlier in the assembly process? A: We need to circularise the contigs and trim overhangs first.

Q: Why can we use some reads (Illumina) to correct other reads (PacBio) ? A: Illumina reads have higher accuracy

Q: Could we just use PacBio reads to assemble the genome? A: Yes, if accuracy adequate.

Short-read assembly: a comparison

So far, we have assembled the long PacBio reads into one contig (the chromosome) and found an additional plasmid in the Illumina short reads.

If we only had Illumina reads, we could also assemble these using the tool Spades.

You can try this here or try it later on your own data.

Get data

We will use the same Illumina data as we used above:

  • illumina_R1.fastq.gz: the Illumina forward reads
  • illumina_R2.fastq.gz: the Illumina reverse reads

Assemble

Run Spades:

spades.py -1 illumina_R1.fastq.gz -2 illumina_R2.fastq.gz --careful --cov-cutoff auto -o spades_assembly_all_illumina
  • -1 is input file of forward reads
  • -2 is input file of reverse reads
  • --careful minimizes mismatches and short indels
  • --cov-cutoff auto computes the coverage threshold (rather than the default setting, “off”)
  • -o is the output directory

Results

Move into the output directory and look at the contigs:

infoseq contigs.fasta

Questions

How many contigs were found by Spades?

  • many

How does this compare to the number of contigs found by assembling the long read data with Canu?

  • many more.

Does it matter that an assembly is in many contigs?

  • Yes

  • broken genes => missing/incorrect annotations

  • less information about structure: e.g. number of plasmids

  • No

  • Many or all genes may still be annotated

  • Gene location is useful (e.g. chromosome, plasmid1) but not always essential (e.g. presence/absence of particular resistance genes)

How can we get more information about the assembly from Spades?

  • Look at the assembly graph assembly_graph.fastg, e.g. in the program Bandage. This shows how contigs are related, albeit with ambiguity in some places.

Next

Further analyses

  • Annotate with Prokka.
  • Comparative genomics, e.g. with Roary.